Atom-Atom Mapping
Given two molecular structures, it is important to identify atoms that are chemically similar. This a commonly used in 3D-QSAR pharmacore analysis, substructure searching, metabolic pathway identification, and chemical machine learning. This problem can be formulated as a 2-sided permutation Procrustes with single transformation.
Permutation Procrustes 2-Sided with Single-Transformation
Given matrix \(\mathbf{A}_{n \times n}\) and a reference \(\mathbf{B}_{n \times n}\), find a permutation of rows/columns of \(\mathbf{A}_{n \times n}\) that makes it as close as possible to \(\mathbf{B}_{n \times n}\), i.e.,
\begin{equation} \underbrace{\text{min}}_{\left\{\mathbf{P} \left| {p_{ij} \in \{0, 1\} \atop \sum_{i=1}^n p_{ij} = \sum_{j=1}^n p_{ij} = 1} \right. \right\}} \|\mathbf{P}^\dagger \mathbf{A} \mathbf{P} - \mathbf{B}\|_{F}^2 \\ \end{equation}
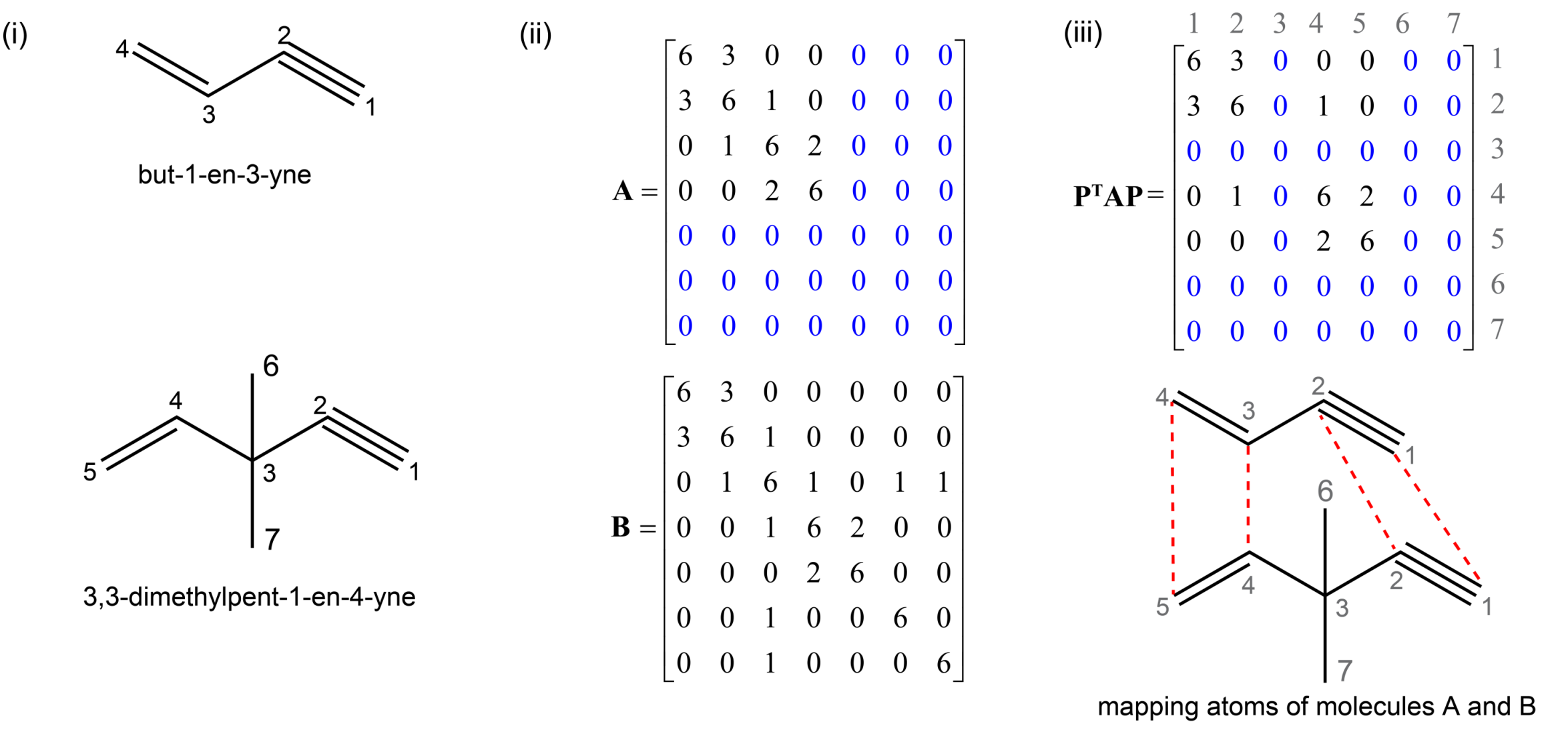
In the code block below, we use the procrustes library to map atoms of but-1-en-3-yne (molecule A) and 3,3-dimethylpent-1-en-4-yne (molecule B) in Fig. (i). Based on our chemical intuition, we can tell that the triple and double bonds of the molecules "match"; however, simple (geometric) molecular alignment based on three-dimensional coordinates does not identify that. The key step is defining a representation that contains bonding information before applying permutation
Procrustes to match atoms.
Fig. (ii): Inspired by graph theory, we represent each molecule with an "adjacency" matrix where the diagonal elements are the atomic numbers and the off-diagonal elements are the bond orders. This results in matrices \(\mathbf{A} \in \mathbb{R}^{4 \times 4}\) and \(\mathbf{B} \in \mathbb{R}^{7 \times 7}\). Note that the permutation Procrustes requires the two matrices to be of the same size, so the smaller matrix \(\mathbf{A}\) is padded with zero rows and columns to have same shape as matrix \(\mathbf{B}\).
Fig. (iii): The mapping between atoms can be also directly deduced from the optimal permutation matrix \(\mathbf{P}\). Specifically, the transformed matrix \(\mathbf{P^{\top}AP}\) should be compared to matrix \(\mathbf{B}\) to identify the matching atoms; the zero rows/columns in \(\mathbf{A}\) (colored in blue) correspond to atoms in \(\mathbf{B}\) for which there are no corresponding atoms.
[1]:
# atom-atom mapping with 2-sided permutation procrustes (with single transformation)
import numpy as np
from procrustes import permutation_2sided
# Define molecule A representing but‐1‐en‐3‐yne
A = np.array([[6, 3, 0, 0],
[3, 6, 1, 0],
[0, 1, 6, 2],
[0, 0, 2, 6]])
# Define molecule B representing 3,3‐dimethylpent‐1‐en‐4‐yne
B = np.array([[6, 3, 0, 0, 0, 0, 0],
[3, 6, 1, 0, 0, 0, 0],
[0, 1, 6, 1, 0, 1, 1],
[0, 0, 1, 6, 2, 0, 0],
[0, 0, 0, 2, 6, 0, 0],
[0, 0, 1, 0, 0, 6, 0],
[0, 0, 1, 0, 0, 0, 6]])
# Two-sided permutation Procrustes (with single transformation)
result = permutation_2sided(A, B, method="approx-normal1", single=True, pad=True)
# Compute the transformed molecule A using transformation matrix P
P = result.t
new_A = np.dot(P.T, np.dot(result.new_a, P)).astype(int)
print("Permutation Matrix:\n", P)
print("\nTransformed A: \n", new_A)
print("\nCompare to Original (padded) B:\n", result.new_b)
print("\nProcrustes Error:", result.error)
Permutation Matrix:
[[1. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0.]
[0. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 0. 1.]]
Transformed A:
[[6 3 0 0 0 0 0]
[3 6 0 1 0 0 0]
[0 0 0 0 0 0 0]
[0 1 0 6 2 0 0]
[0 0 0 2 6 0 0]
[0 0 0 0 0 0 0]
[0 0 0 0 0 0 0]]
Compare to Original (padded) B:
[[6 3 0 0 0 0 0]
[3 6 1 0 0 0 0]
[0 1 6 1 0 1 1]
[0 0 1 6 2 0 0]
[0 0 0 2 6 0 0]
[0 0 1 0 0 6 0]
[0 0 1 0 0 0 6]]
Procrustes Error: 118.0
The corresponding file can be obtained from:
Jupyter Notebook:
Atom_Atom_Mapping.ipynb